Chapter 13 Bayesian linear regression
Learning objectives:
- Understand how to fit a linear model using JAGS
- Learn how to evaluate goodness-of-fit of models using Bayesian p-values
- Be able to calculate confidence and prediction intervals for linear models using JAGS
13.1 Bayesian linear regression
Let’s begin by reconsidering the regression model from Section 1 relating the age of lions to the amount of black pigmentation in their noses:
\[\begin{gather} Age_i \sim N(\mu_i, \sigma^2) \nonumber \\ \mu_i= \beta_0 + \beta_1Proportion.black_i \nonumber \end{gather}\]
Think-pair-share: How many priors will we need to specify when fitting this model?
In this simple model, we have 3 parameters that we will need to specify priors for: \(\beta_0, \beta_1\), and \(\sigma^2\). You might be temped to also list \(\mu_i\), which can be derived from \(\beta_0, \beta_1\), and our data (i.e., proportion.black). In this book, we will try to specify “non-informative” priors for our parameters – meaning that we do not want our choice of prior to have a large influence on our resulting parameter estimates and their uncertainty. This may not always be simple to do, and in general, you will be wise to:
Give careful consideration to the potential values that the parameters may take on and ensure your prior distribution covers this range of values.
Compare prior and posterior distributions to determine if your prior may have been overly constraining or informative (see Exercise 11.3 here).
Try multiple prior distributions as a form of sensitivity analysis (see Exercise 12.2 here).
Using non-informative priors will allow us to generally arrive at similar conclusions when analyzing data using Bayesian and frequentist methods, which will hopefully allow you to gain confidence in using both approaches. Nonetheless, there are certainly other ways to approach Bayesian modeling. In some situations, you may have additional data that you want to have inform your prior distributions (many Bayesians would certainly advocate for such an approach). Historically, priors were sometimes chosen to “play well” with the likelihood of the data - e.g., to give a closed form solution for the posterior distribution. This leads to choosing a conjugate prior - as we did our in initial example in Section 11.3.3. Priors can also influence the choice of MCMC sampling algorithm and the performance of MCMC samplers. We will not cover these topics here, but they can be of extreme importance, especially when constructing more complex models.
For regression parameters in linear regression models, we will usually use “vague” Normal priors48, setting the mean equal to 0 and the precision to a small value (e.g., 0.01 or 0.001, which is equivalent to setting the variance to 100 or 1000). We will generally use uniform \((0, b)\) distributions as a simple and easy way to specify a prior for \(\sigma\). As in our “Bayesian t-test” example from Section 12.4, this prior distribution for \(\sigma\) will induce a prior distribution for \(\tau\), the precision parameter of our Normal distribution.
Below, we specify our JAGS model for the lion data. For now, ignore the code below the likelihood function. We will discuss it when describing a method for performing a goodness-of-fit test for our model (Section 13.3).
#Load packages
library(R2jags) # for interfacing with R
library(MCMCvis) # for summarizing MCMC output
library(mcmcplots) # for plotting MCMC output
library(ggplot2) # for plots
library(patchwork) # for multi-panel plots
theme_set(theme_bw())# Write model
linreg<-function(){
# Priors
beta0 ~ dnorm(0,0.001)
beta1 ~ dnorm(0,0.001)
sigma ~ dunif(0, 100)
# Derived quantities
tau <- 1/ (sigma * sigma)
# Likelihood
for (i in 1:n) {
age[i] ~ dnorm(mu[i], tau)
mu[i] <- beta0 + beta1*proportion.black[i]
}
# Assess model fit using a sums-of-squares-type discrepancy
for (i in 1:n) {
residual[i] <- age[i]-mu[i] # Residuals for observed data
sq[i] <- pow(residual[i], 2) # Squared residuals for observed data
# Generate replicate data and compute fit stats for them
y.new[i] ~ dnorm(mu[i], tau) # one new data set at each MCMC iteration
sq.new[i] <- pow(y.new[i]-mu[i], 2) # Squared residuals for new data
}
fit <- sum(sq[]) # Sum of squared residuals for actual data set
fit.new <- sum(sq.new[]) # Sum of squared residuals for new data set
}We then bundle our data and call JAGS:
#Load the data
library(abd)
data("LionNoses")
# Bundle data
jags.data <- list(age = LionNoses$age,
proportion.black = LionNoses$proportion.black,
n = nrow(LionNoses))
# Parameters to estimate
params <- c("beta0", "beta1", "sigma", "mu", "y.new", "fit", "fit.new", "residual")
# MCMC settings
nc = 3
ni = 2200
nb = 200
nt = 1
# Start Gibbs sampler
lmbayes <- jags(data = jags.data, parameters.to.save = params, model.file = linreg,
n.thin = nt, n.chains = nc, n.burnin = nb, n.iter = ni, progress.bar="none")## Compiling model graph
## Resolving undeclared variables
## Allocating nodes
## Graph information:
## Observed stochastic nodes: 32
## Unobserved stochastic nodes: 35
## Total graph size: 295
##
## Initializing modelLet’s take a look at the output and compare our results to a frequentist analysis using lm:
##
## Call:
## lm(formula = age ~ proportion.black, data = LionNoses)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.5449 -1.1117 -0.5285 0.9635 4.3421
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.8790 0.5688 1.545 0.133
## proportion.black 10.6471 1.5095 7.053 7.68e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.669 on 30 degrees of freedom
## Multiple R-squared: 0.6238, Adjusted R-squared: 0.6113
## F-statistic: 49.75 on 1 and 30 DF, p-value: 7.677e-08## mean sd 2.5% 50% 97.5% Rhat n.eff
## beta0 0.8925477 0.6015003 -0.2886405 0.8904081 2.075223 1.00 6043
## beta1 10.6136759 1.5993293 7.4941599 10.6097754 13.760092 1.00 5306
## sigma 1.7486524 0.2416437 1.3636117 1.7176984 2.296463 1.01 2854We see that we get similar results using both methods. That should be reassuring.
13.2 Testing assumptions of the model
As we saw in Section 1.4, there are lots of different R packages and functions available for creating residual diagnostic plots for linear regression models. We can build similar plots using the output from JAGS, but it is important to recognize that each residual has its own posterior distribution; we will usually want to summarize these posterior distributions using their mean or median values before creating diagnostic plots.
Think-Pair-Share: Why does each residual have a posterior distribution?
Consider this line of code in our JAGS model:
residual[i] <- age[i]-mu[i]
With each chain, we generated ni = 2200 samples from the posterior distribution of beta0 and beta1. Thus, with each chain, we end up with 2200 samples from the posterior distribution of each mu[i] and 2200 samples from the posterior distribution of each residual[i].
The MCMCpstr function in the MCMCvis package (Youngflesh, 2018) provides a convenient way to access the mean (or other summaries) of the posterior distribution for any parameter. Below, we show how to access the posterior mean of the residuals (residual) and fitted values (mu) so that we can create residual versus fitted value plots, QQ-plots for assessing Normality, and a scale-location plot for evaluating homogeneity of variance:
lmresids <- MCMCpstr(lmbayes, params = "residual", func = mean)
lmfitted <- MCMCpstr(lmbayes, params = "mu", func = mean)
jagslmfit <- data.frame(resid = lmresids$residual, fitted = lmfitted$mu)
jagslmfit$std.abs.resid <- sqrt(abs(jagslmfit$resid/sd(jagslmfit$resid)))And, here we create our plots:
p1 <- ggplot(jagslmfit, aes(fitted, resid)) + geom_point() +
geom_hline(yintercept = 0) + geom_smooth()
p2 <- ggplot(jagslmfit, aes(sample = resid)) + stat_qq() + stat_qq_line()
p3 <- ggplot(jagslmfit, aes(fitted, std.abs.resid)) + geom_point() +
geom_smooth() + ylab("sqrt(|Standardized Residuals|)")
p1 + p2 + p3## `geom_smooth()` using method = 'loess' and formula 'y ~ x'
## `geom_smooth()` using method = 'loess' and formula 'y ~ x'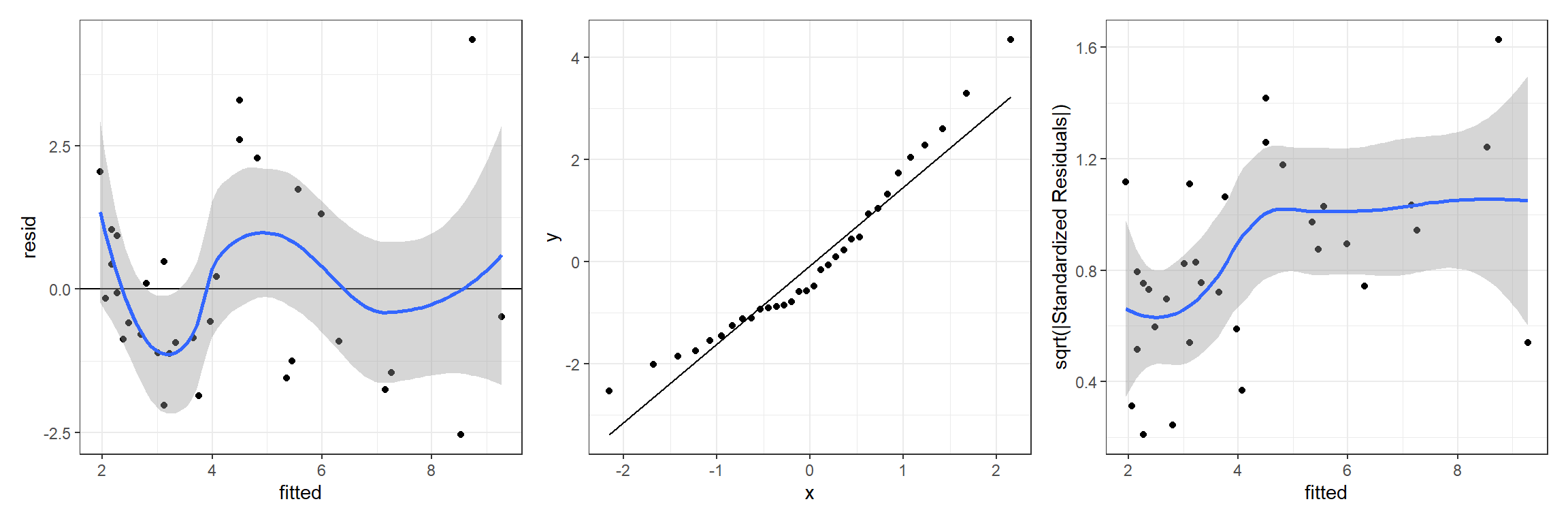
FIGURE 13.1: Residual diagnostic plots for a linear model relating the age of lions to the proportion of their nose that is black fit in a Bayesian framework. Plots depict posterior means of the residual and fitted values.
We can compare Figure 13.1 to similar plots constructed using the output from the frequentist regression using lm (Figure 13.2):
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'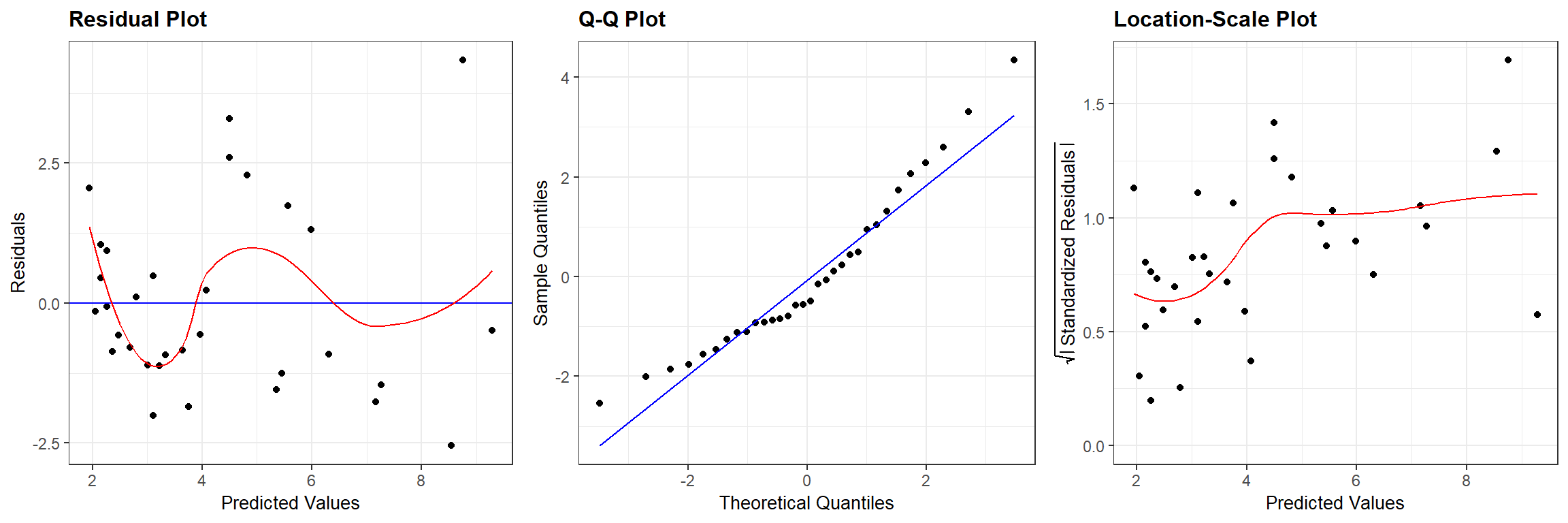
FIGURE 13.2: Residual diagnostic plots associated with a linear model relating the age of lions to the proportion of their nose that is black fit in a frequentist framework.
13.3 Goodness-of-fit testing: The Bayesian p-value
In addition to standard residual plots, it is often useful to conduct a formal goodness-of-fit test when evaluating a fitted model. In this Section, we will demonstrate a common goodness-of-fit test used to evaluate Bayesian models49. Let’s consider the steps involved in any hypothesis test as outlined in Section 1.9.1.
- First, we need to state null and alternative hypotheses. As with any goodness-of-fit test, our hypotheses may be stated as:
- \(H_0:\) the data were generated by the assumed model.
- \(H_A:\) the data were not generated by the assumed model.
- Next, we need a test statistic, \(T\), which will measure the degree to which our data are consistent with the null hypothesis. You are free to choose any test statistic that you want, and if possible, the statistic should capture deviations from the null hypothesis that you deem to be important. For example, one might choose to use the number of zeros in a data set as the test statistic when concerned that data may be zero-inflated (Section 17.2). Here, we will use the sum of squared residuals as a general measure of “fit”:
\[T_{obs} = \sum_{i = 1}^n(Y_i - \hat{Y}_i)^2\]
Next, we need to determine the sampling distribution of the test statistic when the null hypothesis is true. We can generate data sets from our assumed model and calculate \(T\) for each of these data sets to form this sampling distribution.
Lastly, we compare our test statistic calculated using the observed data, \(T_{obs}\), to the sampling distribution of \(T\) when when the null hypothesis is true. The p-value is the probability, when the null hypothesis is true, of getting a test statistic, \(T_{H_0}\), that is as extreme or more extreme than \(T_{obs}\). Ideally, this p-value will be large, suggesting that we do not have much evidence to conclude our assumed model of the data generating process is a poor one.
Now, let’s go back and look at key parts of our specification of the JAGS model, highlighted below:
# Assess model fit using a sums-of-squares-type discrepancy
for (i in 1:n) {
residual[i] <- age[i]-mu[i] # Residuals for observed data
sq[i] <- pow(residual[i], 2) # Squared residuals for observed data
# Generate replicate data and compute fit stats for them
y.new[i] ~ dnorm(mu[i], tau) # one new data set at each MCMC iteration
sq.new[i] <- pow(y.new[i]-mu[i], 2) # Squared residuals for new data
}
fit <- sum(sq[]) # Sum of squared residuals for actual data set
fit.new <- sum(sq.new[]) # Sum of squared residuals for new data setThink-Pair-Share: Which lines of code implement steps 2 and 3 of the hypothesis test?
- We calculate \(T_{obs}\) using:
fit <- sum(sq[]).
- We generate new data sets where the null hypothesis is true using:
y.new[i] ~ dnorm(mu[i], tau) - We calculate \(T_{H_0}\) using:
fit.new <- sum(sq.new[])
There is one new wrinkle in all of this, namely that \(\hat{Y}_i\) has a posterior distribution, which means that \(T_{obs}\) also has a posterior distribution. Our values of \(T_{H_0}\) also account for uncertainty in our estimated parameters. Nonetheless, we can calculate a Bayesian p-value by comparing the posterior distributions of \(T_{obs}\) and \(T_{H_0}\). Specifically, we calculate the Bayesian p-value as:
\[\text{p-value} = \sum_{k=1}^M\frac{T_{H_0}^k \ge T_{obs}^k}{M}\] where \(k\) indexes the \(M\) different posterior samples generated using JAGS. Note, if our model fits poorly, then we should expect that the sums-of-squared residuals associated with our observed data will be large relative to the sums-of-squared residuals for data generated under the assumed model. In this case, \(T_{H_0}^k\) will rarely be greater than \(T_{obs}^k\), we will end up with a small p-value, and we will reject the null hypothesis that the data were generated under the assumed model. If you get a p-value near 0.5, that is ideal as it suggests that the observed data look very similar to the data generated under the assume model (at least when it comes to our chosen test statistic). You might wonder at what point (i.e., what threshold for the p-value) should you become concerned about the reliability of your model. I hesitate to give hard and fast rules, but suggest that a p-value less than 0.05 or 0.1 should give you pause50.
Below, we calculate this p-value for our linear regression model applied to the LionNoses data set by:
- Extracting the MCMC samples using the
MCMCpstrfunction in theMCMCvispackage. - Creating an indicator variable that is equal to 1 whenever \(T_{H_0}^k \ge T_{obs}^k\) and 0 otherwise.
- Calculating the mean of this indicator variable (note, a mean of a 0-1 variable is the same as the proportion of times the variable is equal to 1).
fitstats <- MCMCpstr(lmbayes, params = c("fit", "fit.new"), type = "chains")
T.extreme <- fitstats$fit.new >= fitstats$fit
(p.val <- mean(T.extreme))## [1] 0.5415We see that we have a large p-value, suggesting that we do not have strong evidence that our data was not generated by our assumed model. That is great news, though we need to keep in mind that our power to detect deviations from the null hypothesis may be low due to our small sample size. In addition, because the data are used twice (once to inform the posterior distribution of our model parameters and then to evaluate fit), these tests tend to produce larger p-values than are generally warranted (see e.g., Conn, Johnson, Williams, Melin, & Hooten, 2018).
13.4 Confidence intervals
One of the nice things about Bayesian inference is that we can calculate uncertainty for nearly any quantity using posterior distributions of our model parameters. For example, if we want to get predictions of the mean age of lions at a set of values for proportion.black, we can use the posterior distributions for \(\beta_0\) and \(\beta_1\). Below, we demonstrate how one can accomplish this task using a for loop to get predictions for 10 equally spaced values of proportion.black over the range of the observed data.
First, we pull off and store the MCMC samples of \(\beta_0\) and \(\beta_1\) using the MCMCpstr function with type = "chains" in the MCMCvis package.
We see that we have a total of 6000 MCMC samples from the posterior distribution of \((\beta_0, \beta_1)\) (i.e., 3 chains x 2000 samples per chain):
## [1] 1 6000Next, we create a vector of values for proportion.black for which we desire predictions:
prop.black <-seq(from = min(LionNoses$proportion.black),
to = max(LionNoses$proportion.black),
length = 10)We then loop over the 10 different values of prop.black, estimate the mean age using each of our MCMC samples of \(\beta_0\) and \(\beta_1\), and then find the 2.5 and 97.5 quantiles of the resulting estimates to form our 95% credible interval for each value of prop.black:
# Number of MCMC samples
nmcmc <- dim(betas$beta0)[2]
# Number of unique values of proportion.black where we want predictions
nlions <- length(prop.black)
# Set up a matrix to hold 95% credible intervals for each value of prop.black
conf.int <- matrix(NA, nlions, 2)
# Loop over values for proportion.black
for(i in 1:length(prop.black)){
# Estimate the mean age for the current value of prop.black and for
# each MCMC sample of beta0 and beta1
age.hats <- betas$beta0 + rep(prop.black[i], nmcmc)*betas$beta1
conf.int[i,] <- quantile(age.hats, prob = c(0.025, 0.975))
}Next, we combine our credible interval with predictions for each age using the mean of the posterior distribution of \(\beta_0\) and \(\beta_1\) and plot the results.
beta.hat <- MCMCpstr(lmbayes, params = c("beta0", "beta1"), func = mean)
phats <- data.frame(est = rep(beta.hat$beta0, nlions) + rep(beta.hat$beta1, nlions)*prop.black,
LCL = conf.int[,1],
UCL = conf.int[,2], proportion.black = prop.black)
ggplot(phats, aes(proportion.black, est)) +
geom_ribbon(aes(ymin = LCL, ymax = UCL), fill = "grey70", alpha = 2) +
geom_line() +ylab("Age") +
geom_point(data = LionNoses, aes(proportion.black, age))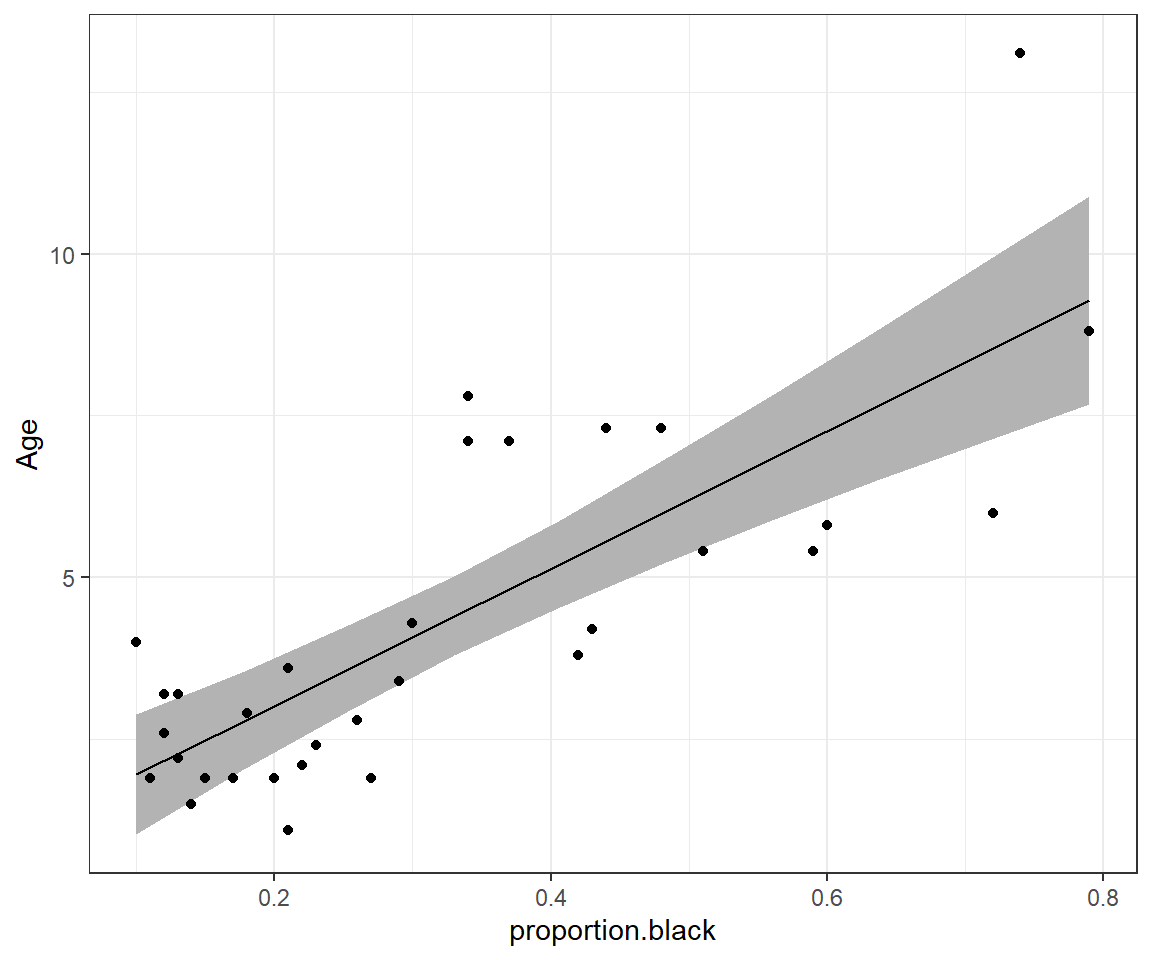
FIGURE 8.2: 95% credible interval for the mean age as a function of proportion.black.
Think-Pair-Share: How could we modify the code in this section to produce a 95% prediction interval?
13.5 Prediction intervals
Recall that prediction intervals need to consider not only the uncertainty associated with the regression line but also the variability of the observations about the line. This variability is modeled using a Normal distribution with standard deviation \(\sigma\). This presents a simple way forward - we just need to simulate added variability about the line using rnorm and can use our posterior distribution for \(\sigma\) when generating these values.
# Pull off the samples from the posterior distribution of sigma
sigmap <- MCMCpstr(lmbayes, params = "sigma", type = "chains")$sigma
# Set up a matrix to hold 95% prediction intervals for each value of prop.black
pred.int <- matrix(NA, nlions, 2)
# Loop over values for proportion.black
for(i in 1:length(prop.black)){
# Estimate the mean age for the current value of prop.black and for
# each MCMC sample of beta0 and beta1
age.inds <- betas$beta0 + rep(prop.black[i], nmcmc)*betas$beta1 +
rnorm(nmcmc, mean = 0, sd = sigmap)
# Now for prediction intervals using the quantiles of the age values
pred.int[i,] <- quantile(age.inds, prob = c(0.025, 0.975))
}Now, we can add the prediction intervals to our plot:
beta.hat <- MCMCpstr(lmbayes, params = c("beta0", "beta1"), func = mean)
phats <- data.frame(phats,
LPL = pred.int[,1],
UPL = pred.int[,2])
ggplot(phats, aes(proportion.black, est)) +
geom_line(aes(proportion.black, LCL), col = "red", lty = 2) +
geom_line(aes(proportion.black, UCL), col = "red", lty = 2) +
geom_line(aes(proportion.black, LPL), col = "blue", lty = 2) +
geom_line(aes(proportion.black, UPL), col = "blue", lty = 2) +
geom_line() +ylab("Age") +
geom_point(data = LionNoses, aes(proportion.black, age))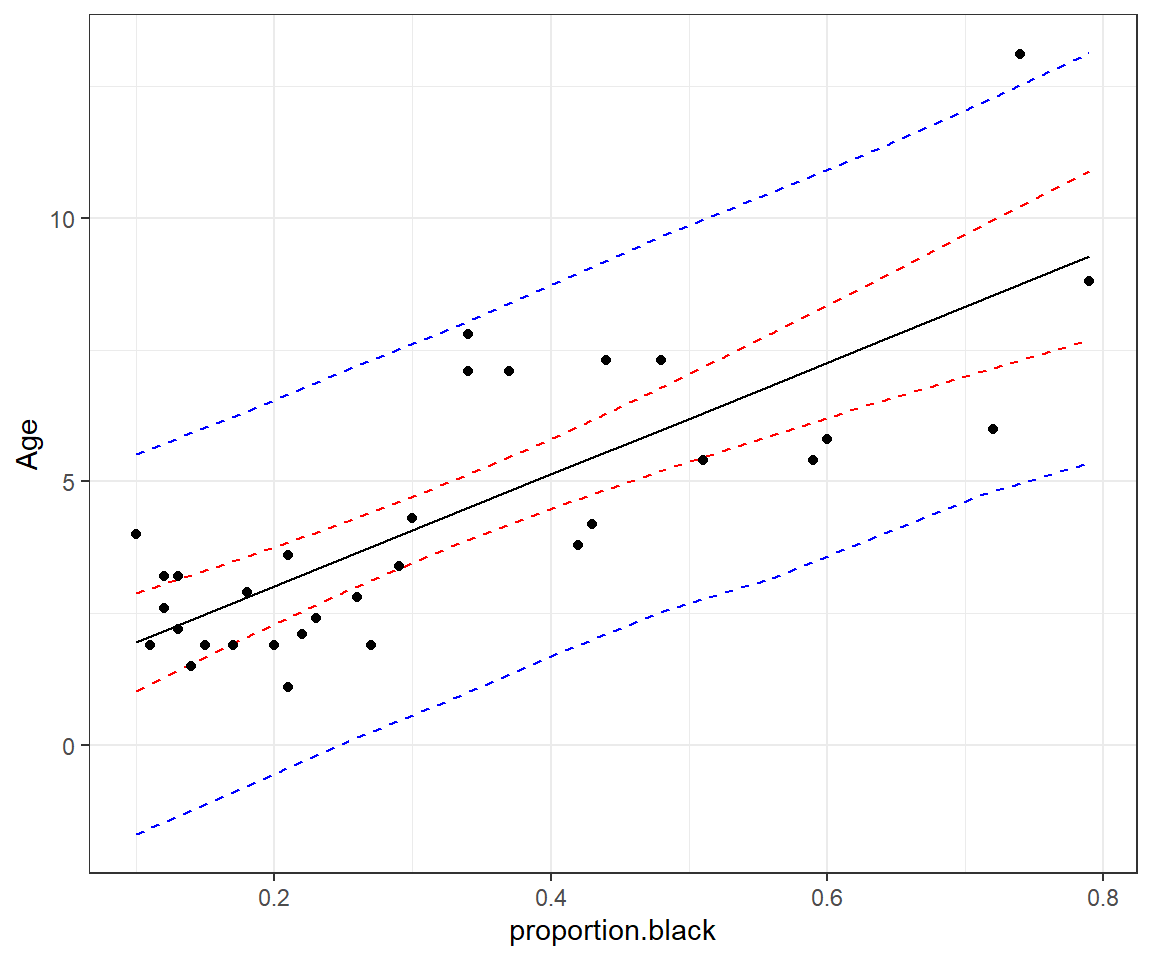
FIGURE 13.3: 95% credible interval for the mean age as a function of proportion.black (red) and prediction interval for a new observation (blue).
13.6 Confidence and prediction intervals the easy way
The above examples are nice in that they demonstrate how you can easily calculate derived quantities using samples from the posterior distributions. However, there is an easier way to get both confidence intervals and prediction intervals - and that is, to have JAGS do all the calculations for us and save the necessary output.
If we look at our JAGS code, below, we actually had everything we needed to calculate confidence intervals and prediction intervals.
Think-Pair-Share: Can you think of an easier way to calculate confidence intervals and credible intervals from quantities that JAGS is already computing?
linreg<-function(){
# Priors
beta0 ~ dnorm(0,0.001)
beta1 ~ dnorm(0,0.001)
sigma ~ dunif(0, 100)
# Derived quantities
tau <- 1/ (sigma * sigma)
# Likelihood
for (i in 1:n) {
age[i] ~ dnorm(mu[i], tau)
mu[i] <- beta0 + beta1*proportion.black[i]
}
# Assess model fit using a sums-of-squares-type discrepancy
for (i in 1:n) {
residual[i] <- age[i]-mu[i] # Residuals for observed data
sq[i] <- pow(residual[i], 2) # Squared residuals for observed data
# Generate replicate data and compute fit stats for them
y.new[i] ~ dnorm(mu[i], tau) # one new data set at each MCMC iteration
sq.new[i] <- pow(y.new[i]-mu[i], 2) # Squared residuals for new data
}
fit <- sum(sq[]) # Sum of squared residuals for actual data set
fit.new <- sum(sq.new[]) # Sum of squared residuals for new data set
}Note that:
- JAGS has already sampled from the posterior distribution of the mean age for the values of
proportion.blackin our data set – i.e.,mu[i]. - JAGS has already generated new observations from our assumed model – i.e.,
y.new[i]. These can be used to form prediction intervals.
Below, we demonstrate that these outputs could be used to form confidence and prediction intervals.
CI <- MCMCpstr(lmbayes, params = c("mu"),
func = function(x) quantile(x, probs = c(0.025, 0.975)))$mu
PI <- MCMCpstr(lmbayes, params = c("y.new"),
func = function(x) quantile(x, probs = c(0.025, 0.975)))$y.newPlotting these results, we see that we get nearly identical intervals as in Figure 13.3:
phats2 <- data.frame(est =MCMCpstr(lmbayes, params = c("mu"), func = mean)$mu,
proportion.black = LionNoses$proportion.black,
LCL = CI[,1],
UCL = CI[,2],
LPL = PI[,1],
UPL = PI[,2])
ggplot(phats2, aes(proportion.black, est)) +
geom_line(aes(proportion.black, LCL), col = "red", lty = 2) +
geom_line(aes(proportion.black, UCL), col = "red", lty = 2) +
geom_line(aes(proportion.black, LPL), col = "blue", lty = 2) +
geom_line(aes(proportion.black, UPL), col = "blue", lty = 2) +
geom_line() +ylab("Age") +
geom_point(data = LionNoses, aes(proportion.black, age))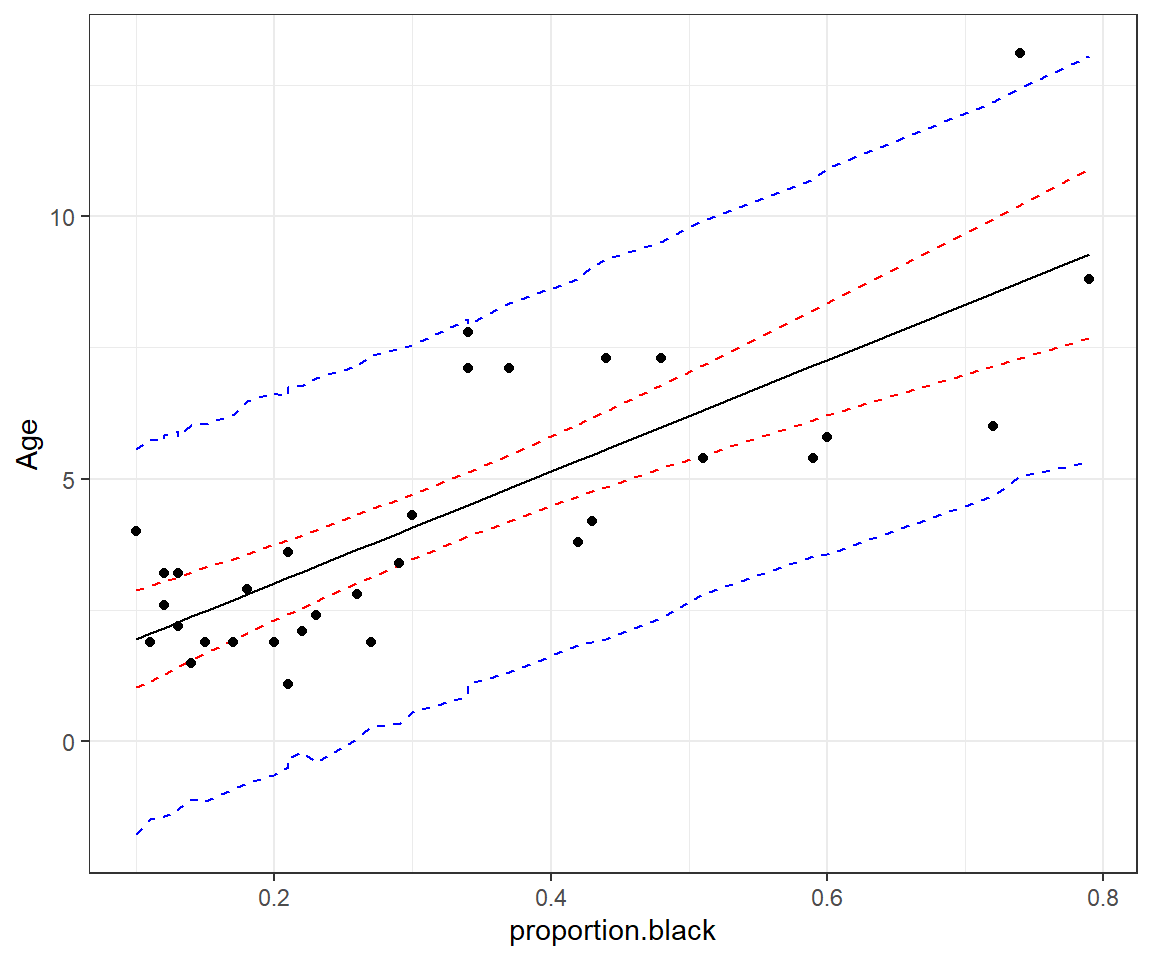
FIGURE 13.4: 95% credible interval for the mean age as a function of proportion.black (red) and prediction interval for a new observation (blue).
The meaning of vague here is that the prior distribution allows for a wide range of potential values.↩
A similar approach can be implemented for frequentist models as we will see in Section 15.3.5↩
Note that it is possible, though fairly unlikely, that a model will fit the observed data much better than data generated from the assumed model, resulting in a Bayesian p-value that is close to 1. In this case, it is also worth digging a little deeper to see why this may be the case.↩